几何画板怎么证明勾股定理 证明方法介绍

几何画板作为专业的几何绘图工具，不仅仅可以用它绘制一些几何图形，同时还可以用它来证明一些几何定理结论，那么几何画板如何证明勾股定理呢？接下来小编就为大家带来解答。

具体的制作步骤如下：

步骤一 绘制三角形

1.打开几何画板，首先需要制作一个直角三角形，单击左边侧边栏“自定义工具”按钮，在弹出的工具菜单选择“三角形”——直角三角形，如下图所示。

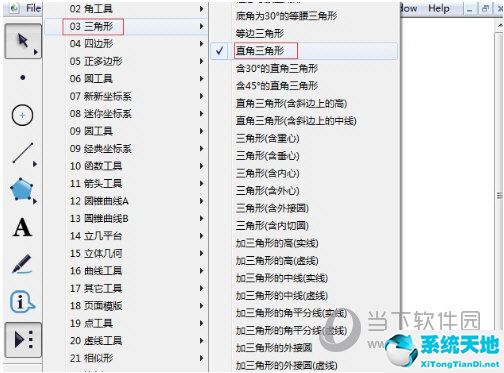
2.工具选好后，在画布上面单击一下，画出直角顶点，然后再拖动鼠标，在适当的地方再次单击鼠标画出一个直角三角形，选择左边侧边栏“文字工具”依次给三条边并命名a、b、c，如下图所示。

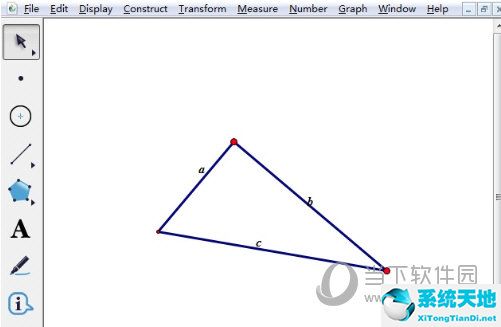
步骤二 度量边长

选择侧边栏“移动箭头工具”选定直角边a，并单击上方菜单栏“度量”菜单，在其下拉菜单选择“长度”，这样就可以看到直角边a的长度已经求出来了。用同样的方法度量出b边和c边的长，如下图所示。

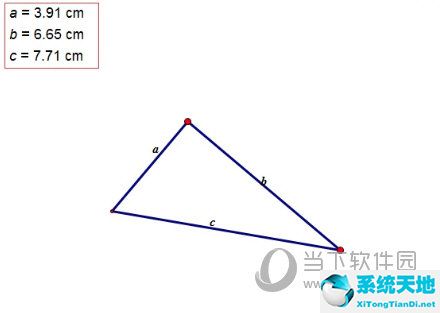
步骤三 证明勾股定理

1.用勾股定理来求一下c边看看求出的结果如何。单击上方菜单栏“数据”菜单，在其下拉菜单选择“计算”，在出现的对话框中输入勾股定理并单击“确定”按钮，如图所示。

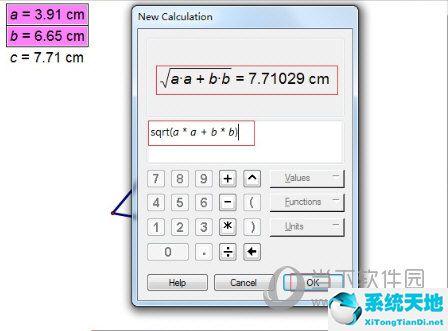
2.现在我们可以看到用勾股定理求出的c边值如下图所示，发现和度量的c边的值是一样的，这样就证明了勾股定理的正确性。

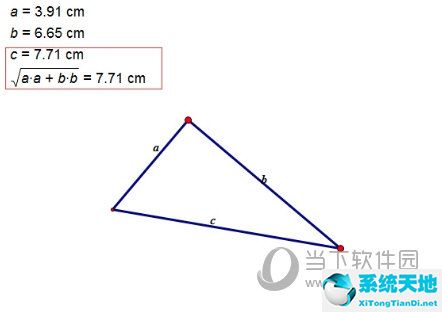
以上给大家讲解了用几何画板证明勾股定理的方法，主要运用了几何画板度量菜单，利用勾股定理公式计算斜边的长度，从而验证了该定理的成立性，从而更形象地让学生们掌握了该定理。